3D Object Representation
computational algorithm, application to simulation and robotics
3D object representation is an important topic in robotics, simulation, and graphics. Various representation schemes come with trade-offs and are typically designed for specific applications. Our focus is on representations tailored for robotics problems involving contact.
Shape Abstraction via Differentiable Convex Geometries
Object representations are often derived from raw sensory data, such as images or point clouds, or transformed from dense, unstructured information. Shape abstraction refers to the process of converting these low-level representations into more structured and usable forms. We employ a differentiable convex representation as the foundational unit for this abstraction.
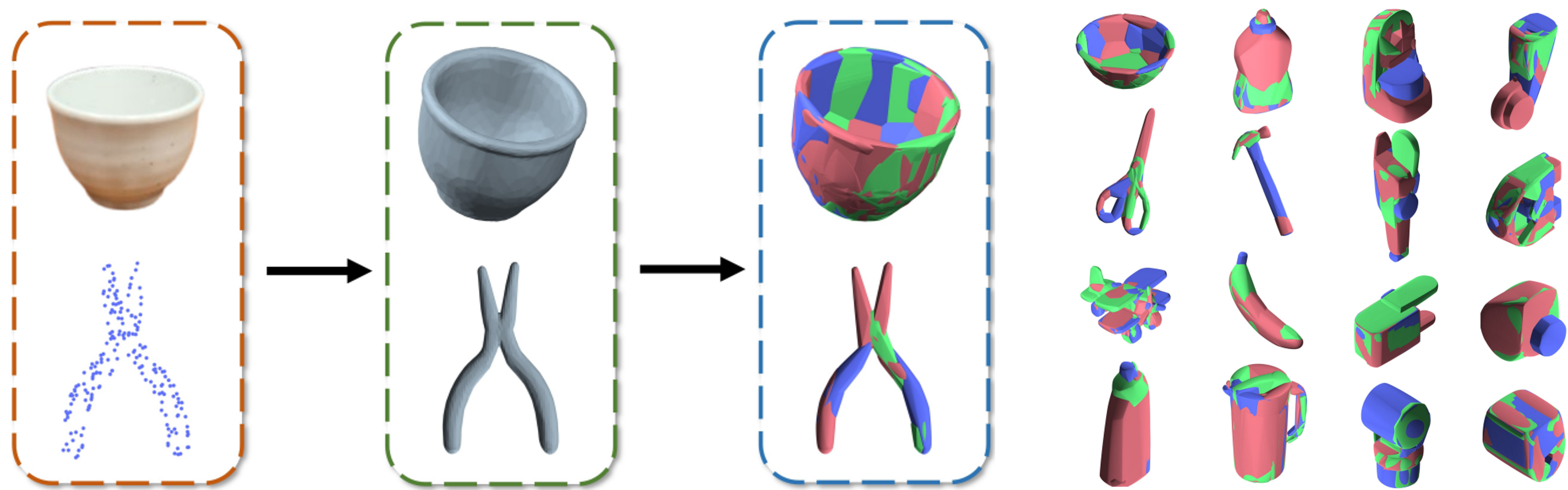
The abstraction results can be forwarded to efficient contact computation algorithm and directly applied to physics simulation, planning, contact localization problems, and more.
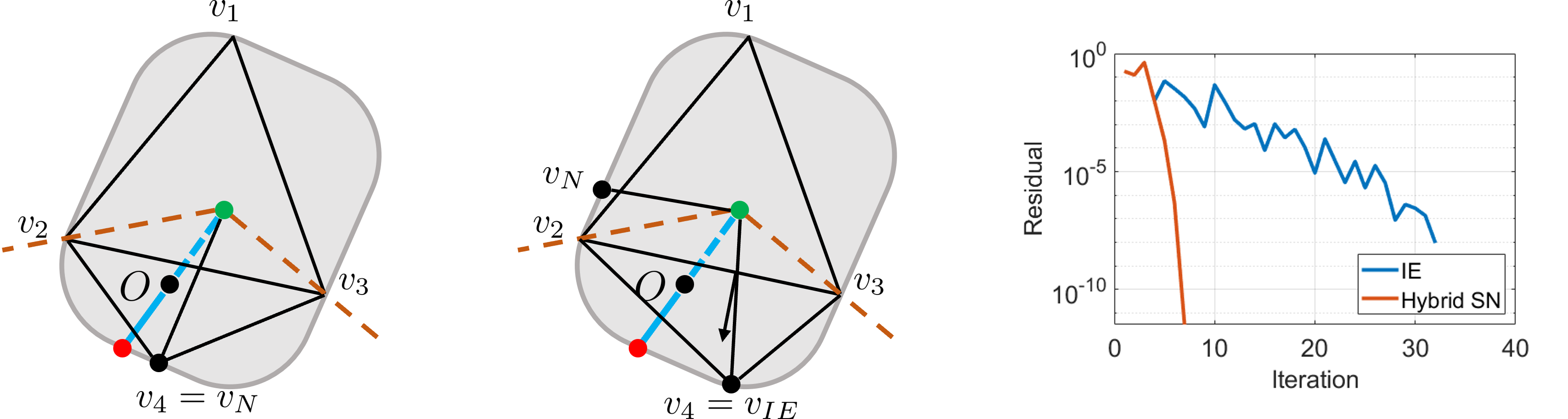
Differentiable Support Function
A key step in simulation and robotics is computing contact features—such as distance, contact points, and normals—from given object representations and poses. The Differentiable Support Function (DSF) is designed to handle a wide range of convex geometries while ensuring the differentiability of these contact features.

Such properties of DSF can be utilized in gradient-based solution of diverse estimation and planning with contact. Here is an example:
